FRACTAL

Un fractal es un objeto geométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas. El término fue propuesto por el matemático BENOIT MANDELBROT  en  1975 y deriva del Latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal. La propiedad matemática clave de un objeto genuinamente fractal es que su dimensión métrica fractal es un número no entero.
Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos DIMENSION  FRACTAL fueron establecidas a principios del siglo XX en el seno de la TEORIA DE LA MEDIDA.

Los ejemplos clásicos

Para encontrar los primeros ejemplos de fractales debemos remontarnos a finales del siglo XIX: en 1872 apareció la función de Weierstrass, cuyo grafo hoy en día consideraríamos fractal, como ejemplo de función continua pero no diferenciable en ningún punto.

  1º EJEMPLO:         Alfombra de Sierpinski
   La alfombra de Sierpiński es un conjunto fractal descrito por primera vez por Wacław Sierpiński en 1916. Constituye una generalización a dos dimensiones del conjunto de Cantor. Comparte con él muchas propiedades: también es un conjunto compacto, no numerable y de medida nula.

Construcción

La construcción de la alfombra de Sierpinski se define de forma recursiva:

1. Comenzamos con un cuadrado.
2. El cuadrado se corta en 9 cuadrados congruentes, y eliminamos el cuadrado central.
3. El paso anterior vuelve a aplicarse recursivamente a cada uno de los 8 cuadrados restantes.

La alfombra de Sierpinski es el límite de este proceso tras un número infinito de iteraciones.

Construcción de la alfombra de Sierpinski:

2º EJEMPLO:

Los conjuntos de Julia

Estos conjuntos, fruto de los trabajos de PIERRE  FATOU y GASTON JULIA en los ANÑO 1920 , surgen como resultado de la aplicación reiterada de FUNCIONES HOLOMORFAS.
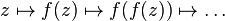Analicemos el caso particular de funciones polinómicas de grado mayor que uno. Al aplicar sucesivas veces una función polinómica es muy posible que el resultado tienda a . Al conjunto de valores de que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de julia.
Estos conjuntos se representan mediante un algoritmo de tiempo de escape, en que cada pixel se colorea según el número de iteraciones necesarias para escapar. Suele usarse un color especial, a menudo el negro, para representar los puntos que no han escapado tras un número grande y prefijado de iteraciones.